© Spectrum of Science (detalles)
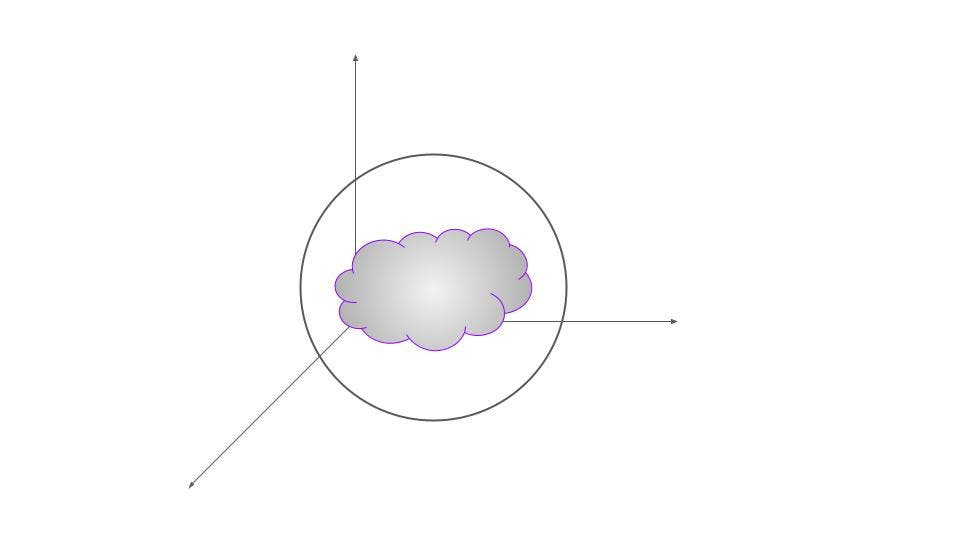
conjunto comprimido | Normalmente, los grupos comprimidos siempre se pueden poner en una esfera.
Pero no sólo es extraño el espacio de cuatro dimensiones en sí mismo, también lo son las formas de cuatro dimensiones. Imagina que vives en un mundo de cinco dimensiones y quieres ordenar las superficies de cuatro dimensiones: ¿cuál es diferente de la otra? ¿Qué clases de techos hay? Para entender esto, es más fácil comenzar con nuestro familiar mundo tridimensional.
Allí podemos examinar superficies bidimensionales, como superficies esféricas o un toro. Al final resultó que, todas las superficies 2D (cerradas) se dividen en solo tres clases, como Henry Poincaré demostrado ya en 1907: son equivalentes (de varias formas) a una superficie esférica, tortas que se pegan, o a superficies salientes que se pegan (que, por ejemplo, botella de klein contar). Sin embargo, no importa cuán compleja pueda parecer una forma 2D, siempre se puede reconfigurar en una de las tres categorías, y sin problemas.
Si vivieras en la cuarta dimensión y observaras superficies tridimensionales, habría ocho categorías diferentes: puedes reducir cualquier superficie tridimensional a ocho formas básicas. Esto era Guillermo Thurston Se sospecha de 1982, pero la llamada geometría triple era solo eso. Probado por Grigori Perelman en 2003que, por cierto, también Conjetura de Poincaré Demostrar: cualquier superficie 3D sin un agujero se puede deformar en una superficie 3D esférica. El resultado muestra que también existe un esquema de clasificación para superficies 3D.
Si vas a dimensiones más altas y quieres examinar superficies en cinco o seis dimensiones o incluso más, se vuelve más difícil. ¿Cómo clasificamos cosas tan complejas? Lo que los matemáticos suelen usar para esto es el llamado metodo whitney: Uno puede imaginarse arrojando un lazo alrededor de una figura y comprobando si la superficie tiene agujeros en función del comportamiento cuando se juntan. Como ya se mencionó, la pelota se puede distinguir del aro de esta manera. Mientras que cualquier lazo cerrado en la esfera puede contraerse hasta un punto, el lazo no puede. Esto también funciona bien para superficies que contienen más de cuatro dimensiones. Cuando aprietas la cuerda, se crea un área de disco circular. Para poder determinar qué tipo de superficie está mirando, debe examinar por separado todos los tipos posibles de discos resultantes. Sin embargo, las áreas del lazo pueden superponerse, lo que es problemático desde un punto de vista matemático. por norte > 4 Uno puede usar las dimensiones adicionales para separar dos partes entre sí. Esto es similar al proceso cuando desea separar dos líneas rectas que se cruzan en un plano: esquivar izquierda/derecha o arriba/abajo no hace nada. La única forma de separar líneas rectas a través de la profundidad es agregar una tercera dimensión espacial. Lo mismo funciona en cinco dimensiones con discos bidimensionales. De esta forma, el método del lazo se puede utilizar para identificar superficies de cinco o más dimensiones que son anisótropas entre sí.
© Spectrum of Science (detalles)
lineas rectas | Si desea separar dos líneas que se cruzan, necesita una tercera dimensión espacial.
Así que ha encontrado todas las categorías con superficies bidimensionales, tridimensionales, pentagonales y multidimensionales. Y es posible que lo hayas adivinado: la cuarta dimensión está causando dificultades nuevamente. Porque resulta que es imposible clasificar criaturas tetragonales de diferentes formas: ¡este mundo es un desastre absoluto!
El mundo de cuatro dimensiones también contiene un secreto, según el topólogo Ciprian Manolescu, el problema más importante en topología: ¿puede cada superficie de cuatro dimensiones sin un agujero deformarse de manera diferente en una superficie esférica de cuatro dimensiones? Esta es una conjetura suave de Poincaré. La conjetura habitual de Poincaré ya se ha utilizado para todas las dimensiones. norte Probado, pero solo en un sentido topológico general: también se permiten deformaciones que causan ángulos y bordes. Así que los topólogos están interesados en cómo norteLa conjetura dimensional de Poincaré falla si solo se permiten diferentes distorsiones de forma. Mientras tanto, han encontrado una respuesta para cada dimensión del espacio, excepto norte . de esquinas y bordes. Para todas las demás dimensiones, también se puede calcular el número de esferas impares, que a veces puede ser muy grande. Hasta ahora, no se ha encontrado ningún objeto en cuatro dimensiones que no tenga un agujero y no difiera en forma en una esfera, pero tampoco ha sido posible probar que ninguno de ellos existe.

«Alborotador. Amante de la cerveza. Total aficionado al alcohol. Sutilmente encantador adicto a los zombis. Ninja de twitter de toda la vida».