Las señales cortas conducen a la incertidumbre de la indecisión
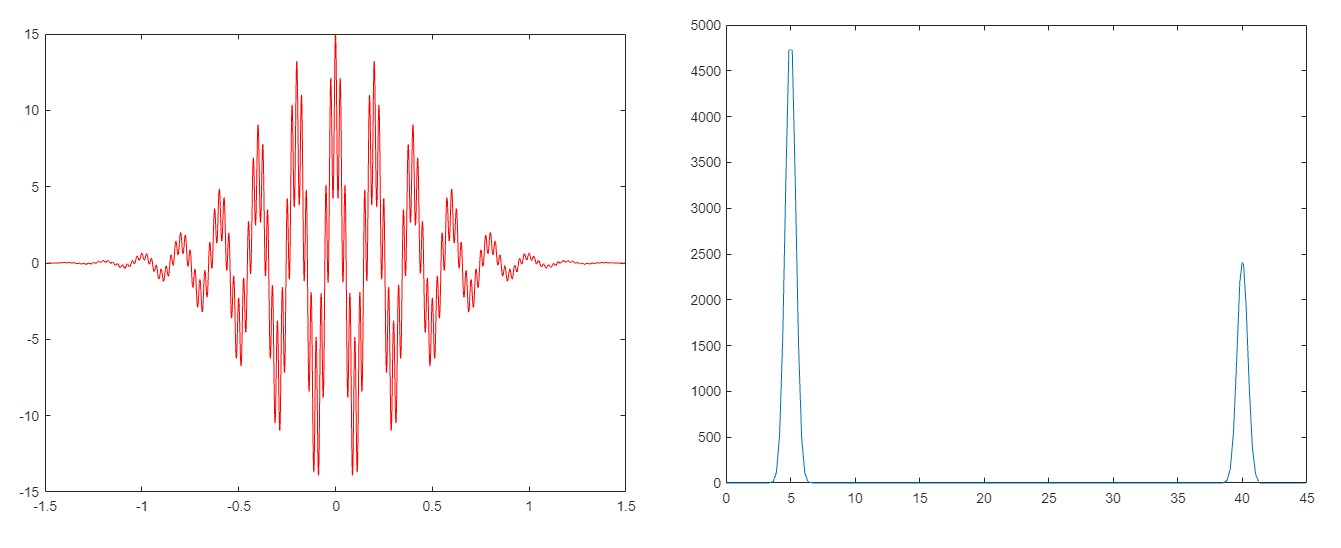
Digamos que grabaste una señal corta de dos frecuencias k = 5 Hzf k = 40 Hz. Entonces, la función tiene la siguiente forma, por ejemplo: \(f
Señal y transformada de Fourier
De esta manera uno puede usar la transformada de Fourier para cualquier función y T) Calcular. Y puedes probarloQue el principio de incertidumbre ocurre inevitablemente: cuanto más corta es la señal de tiempo, más anchos son los picos en el rango de frecuencia, se manchan hasta cierto punto. Esto significa que los componentes de frecuencia de la señal no pueden identificarse claramente. Por el contrario, la señal se amplía con el tiempo a medida que las frecuencias se seleccionan con mayor precisión.
Uno puede usar este camuflaje para funciones generales. y T) probarlo, pero esto requiere conocimientos de análisis armónico. Pero podemos calcular la ambigüedad usando el ejemplo anterior reemplazando el factor \(e^{-\pi t^2}\) con \(e^{-\pi \cdot A \cdot t^2}\)., por a es un numero grande el mas grande acuanto más corta sea la señal y T). Si realiza la transformada de Fourier como antes, obtiene el siguiente resultado: \(\frac{5}{\sqrt{A}}\left(2e^{-\frac{\pi }{A}(k-5) )^ 2} + e^{-\frac{\pi }{A}(k-40)^2} \right)\). El trabajador a Ahora aparece como un recíproco en la función, lo que hace que la curva asociada con él se ensanche en el dominio de la frecuencia.
Cristal de Fourier | Cuanto más corta es la señal, más ancha es la distribución de frecuencias y viceversa.
Esto explica por qué tiene que decidirse por mediciones de radar normales: o envía un pulso muy corto a la ubicación más precisa posible, lo que, sin embargo, desdibuja el espectro de frecuencia. En este caso, es difícil estimar la velocidad de un objeto en movimiento. Y viceversa, también puede usar una señal más larga, lo que hará que la medición de la ubicación sea menos precisa; Sin embargo, los componentes de frecuencia son más pronunciados, lo que resulta en una mejor limitación de velocidad.
Esta elección entre una medida exacta de posición o velocidad recuerda mucho al principio de incertidumbre de Heisenberg de la mecánica cuántica. El problema es similar allí, porque los objetos de la mecánica cuántica como los electrones o los átomos ya no pueden describirse como partículas puntuales puras. Como descubrieron los físicos a principios del siglo XX, las partículas también tienen propiedades ondulatorias. Esto conduce directamente al principio de incertidumbre: es imposible determinar la posición y la velocidad de una partícula mecánica cuántica con cualquier grado de precisión al mismo tiempo. Así, el principio de incertidumbre no es una especificidad de la física cuántica, sino una parte integral de nuestro mundo, que también se expresa en problemas prácticos como el posicionamiento del radar.