Teoría de grupos para principiantes.
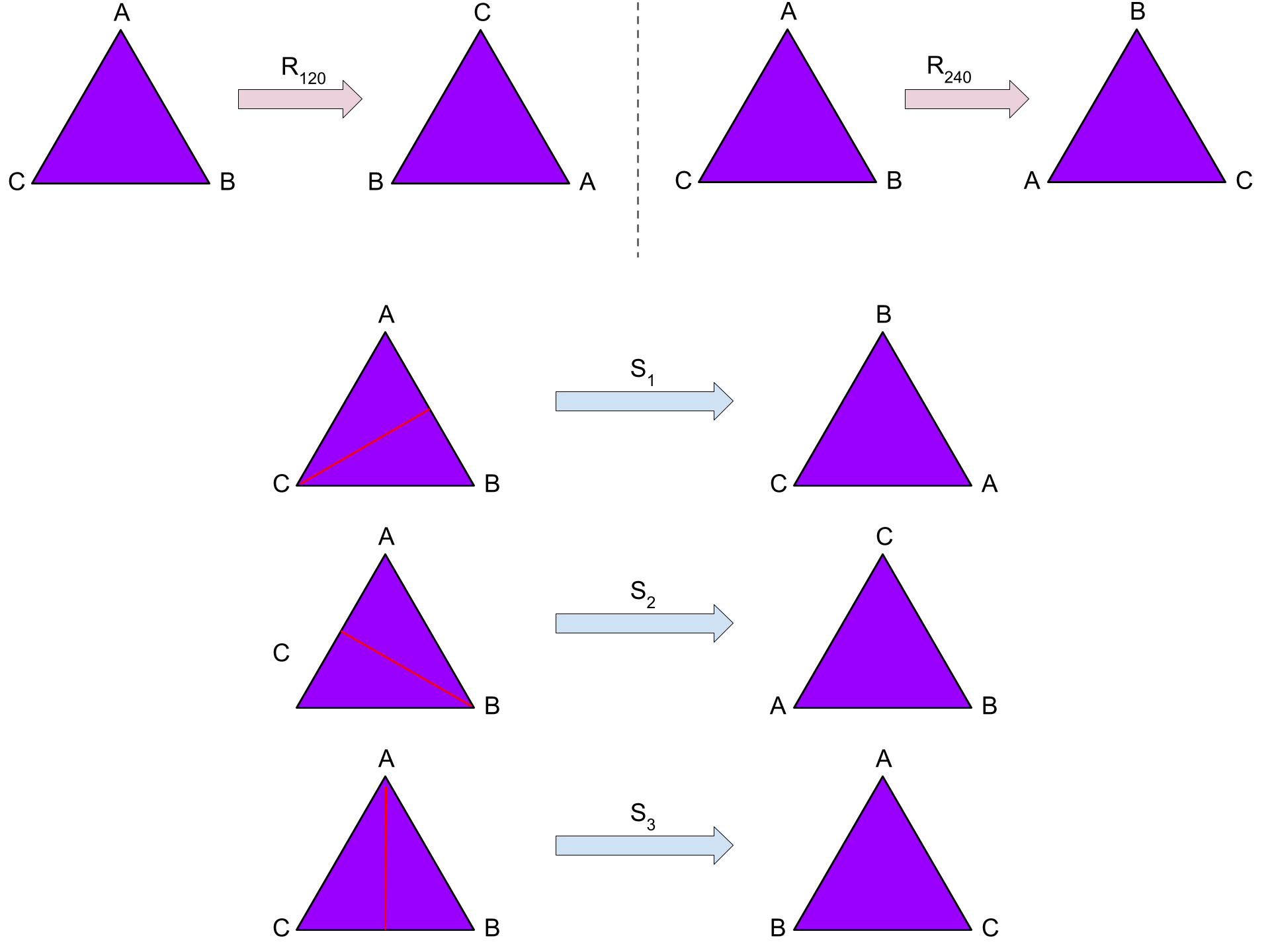
La forma más sencilla de visualizar el grupo es como un conjunto de transformaciones de simetría. Por ejemplo, si giras un triángulo equilátero 120 grados, su forma no cambia. Un triángulo de este tipo se puede girar en tres ángulos totales (0°, 120° y 240°). Cada uno de estos ciclos es una transformación analógica. Juntos forman un grupo limitado.
Además de la rotación, un triángulo también puede reflejarse a lo largo de su eje central. Las rotaciones y reflexiones se mencionan como cada forma de «subconjunto» del grupo de simetría completo del triángulo.
© Espectro de la ciencia / Manon Bischof (detalle)
Simetrías de triángulos | Las simetrías del triángulo forman un grupo finito.
Estrictamente hablando, un grupo se define de manera más abstracta. Define un conjunto cuyos elementos se ajustan a ciertas reglas: la combinación de dos elementos (por ejemplo, realizar dos giros uno tras otro) debe dar como resultado el elemento del conjunto. Cada grupo también contiene un «elemento neutral» que deja todos los demás elementos sin cambios, como multiplicar por uno o sumar por cero. Además, cada elemento también debe tener una contraparte (el «elemento inverso») para que la combinación de los dos elementos cree nuevamente el elemento neutral; por ejemplo, debe poder realizar cada rotación en la dirección opuesta.
© Espectro de la ciencia / Manon Bischof (detalle)
Conexiones
No importa cuáles sean exactamente los elementos del grupo. Pueden incluir transformaciones de simetría como rotaciones y reflexiones, pero también números. Por ejemplo, los números racionales forman un grupo con la multiplicación: la suma (producto) de dos números racionales siempre produce un resultado racional; El elemento neutro es uno y el elemento opuesto es el recíproco del número.
Todas las operaciones de simetría de un objeto determinado (como una figura geométrica) se pueden combinar en lo que se llama un conjunto. Esto elevó las matemáticas, especialmente el campo del álgebra, al nivel abstracto. De repente ya no se trataba de las cosas en sí mismas (formas geométricas, números o ecuaciones) sino de sus relaciones entre sí.
Para los físicos interesados en resultados concretos, la teoría de grupos era inicialmente un libro cerrado. Muchos conceptos parecían tan abstractos que tenían pocas aplicaciones claras. Esto cambió cuando en la década de 1930 el físico Eugene Wigner, y más tarde Gell-Mann, se dieron cuenta de los enormes beneficios de la teoría en la física.
Representaciones grupales
Un conjunto es inicialmente un conjunto: una colección de objetos. Pero cada grupo en realidad tiene una representación, lo cual es muy útil para visualizar conceptos abstractos. La idea detrás de esto: dibujas un punto en un sistema de coordenadas y luego le aplicas elementos de grupo que mueven el punto en el plano. Por ejemplo, si el conjunto contiene una reflexión, el punto se refleja a lo largo del eje. Grabar el movimiento del punto produce un patrón simétrico que representa el efecto de grupo.
Desde una perspectiva matemática, un conjunto puede representarse como un conjunto de matrices (una tabla). Pero resulta que esta representación no está clara. Por ejemplo, algunos conjuntos pueden representarse mediante varias matrices de 3×3, pero también mediante matrices de 8×8. Ambas variables reflejan cambios de simetría del grupo.
Estas diferentes representaciones proporcionan patrones distintos para cada grupo. En el caso del llamado conjunto SU(3), los patrones de puntos en una representación (con matrices de 3×3) corresponden a octetos, y en la siguiente representación más grande (con matrices de 8×8) corresponden a un conjunto binario: los patrones descritos de Gell-Mann han sido registrados. Para decirlo sin rodeos, SU(3) significa que existe una similitud entre tres objetos diferentes. Si eliges una partícula en el octeto de Gelman y le aplicas la transformación de simetría SU(3), es decir, reemplazas uno de los tres elementos por otro, inevitablemente terminarás con una partícula diferente en el octeto. Entonces la pregunta era: ¿Cuáles son las tres cosas que crean simetría?
Junto con su colega Georg Zweig, Gell-Mann formuló una hipótesis audaz: estos objetos podrían ser partículas elementales desconocidas. Los dos físicos propusieron que el protón, el neutrón, los kaones y el resto del jardín de partículas no son elementos elementales en absoluto, sino que están compuestos por los mismos tres bloques básicos: los «quarks». Estos deben ocurrir en tres especies diferentes y así producir la simetría SU(3) observada. Al nombrarlo, Gilman se inspiró en la novela Finnegan's Wake de James Joyce, que dice: «¡Tres quarks para Muster Mark!»

«Alborotador. Amante de la cerveza. Total aficionado al alcohol. Sutilmente encantador adicto a los zombis. Ninja de twitter de toda la vida».